8. lecke |
9. lecke |
|---|

7. lecke - Fraktálok
 |
 |
 |
BEVEZETŐ - MiI IS AZ A FRAKTÁL?
A fraktálok a matematikatörténet során már az 1880-as évektől kezdve fellelhetőek, igaz, csak mint egyedülálló, egymástól elszigetelt matematikai érdekességek és ellenpéldák. Jelentőségükre Benoit B. Mandelbrot amerikai matematikus figyelt fel, ő gyűjtötte ezeket a matematikai "kakukktojásokat" egy csoportba, és ő nevezte el őket 1975 körül fraktáloknak. A fraktál szó a latin fractus szóból származik, melynek jelentése törött, töredezett. Olyan alakzatokat, ponthalmazokat nevezett így, melyek lényegesen szabálytalanabbak, összetettebbek, töredezettebbek a klasszikus geometriában előforduló alakzatoknál.
Érdekes tény, hogy a fraktáloknak pontos matematikai definícója a mai napig nem létezik. Többen próbálkoztak már a definíció megfogalmazásával (elsősorban természetesen maga Mandelbrot), de minden esetben lehetett találni egy fraktált vagy fraktálcsoportot, melyre a definíció nem illett. Ezért aztán Mandelbrot és később Kenneth J. Falconer azt javasolta, ne is adjunk definíciót a fraktál fogalmára, hiszen a természetben is oly sok nem pontosan definiálható jelenség létezik, például akár maga az élet. Falconer definíció helyett a legfontosabb tulajdonságokat fogalmazta meg, melyek alapján egy halmazt illetve alakzatot fraktálnak tekinthetünk, ezek között a tulajdonságok között szerepel például, hogy "finom struktúrája van", vagy hogy "túl szabálytalan ahhoz, hogy leírható legyen a klasszikus geometriában".
A fraktálok világa hihetetlenül változatos. Az ebben a leckében található fraktálok a legegyszerűbbek, egyszerű rekurzív szabállyal előállíthatóak. Azonban például az internetes fraktálgalériákban milliószámra találhatunk olyan gyönyörű, színes fraktálokat, melyek első ránézésre inkább festménynek tűnnek, és nem matematikai alakzatnak.
A fraktálok furcsasága, hogy igazi fraktált nem lehet a valóságban előállítani, mert a fraktálok körvonala mindig a végtelenségig finomodik, csipkéződik. Még ha egyszerű szabállyal megadható is az előállításuk (ahogyan az ebben a leckében található példák mindegyikén látjuk majd), akkor is előállításukhoz végtelen lépésre lenne szükség. Ehhez nem csak végtelen sok idő kellene, de véges eszközökkel (mint a számítógép képernyőjének felbontása) a végtelenségig finomodó vonalak kirajzolása is lehetetlen. Ezért a fraktálokat teljes valóságukban csak elképzelni lehet, illetve meglévő eszközeinkkel közelíthetjük kinézetüket.
CANTOR-POR
Előállítás szempontjából a legegyszerűbb egyben a legrégebben felfedezett fraktál a Cantor-halmaz vagy Cantor-por. 1883-ban jelentette meg Georg Cantor.
A Cantor-por előállítása:
0. lépés: vegyünk egy szakaszt
1. lépés: vágjuk ki a középső egyharmadát
2. lépés: a keletkezett két szakasznak is vágjuk ki a középső egyharmadát
3. lépés: a keletkezett összes szakasznak vágjuk ki a középső egyharmadát
És így tovább. Amit végtelen lépés után kapnánk, az a Cantor-halmaz, vagy Cantor-por.
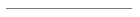
|

|

|

|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés |
Ez egyszerű eljárásnak tűnik, papíron könnyedén lerajzolhatjuk a Cantor-por közelítését jónéhány lépésen keresztül, de hogyan valósítható ez meg LOGO-ban?
Vegyük észre, hogy tulajdonképpen nem történik más, mint minden lépésben a meglévő szakaszokat kicseréljük olyan szakaszokra, melyeknek a közepe "ki van harapva". Vagyis ahelyett, hogy az előző lépésben szereplő folytonos szakaszt megrajzolnánk, egy harmadakkora szakaszt rajzolunk, majd felemeljük a tollat, és egyharmad szakasznyit így megyünk előre, aztán letesszük a tollat, és újra rajzolunk egy egyharmad hosszú szakaszt. Ennek megvalósításához segítségül hívjuk a korábbiakban megismert rekurziót.
Az eljárásnak két paramétere lesz, a lépésszám, és a kezdő szakasz hossza. Az alapötlet az, hogy ha a lépésszám 0, akkor a teknőcnek nincs más teendője, mithogy rajzoljon egy szakaszt. Ha nem 0, akkor "kiharapott" szakaszt kell rajzolnia. A "kiharapott" szakasz pedig úgy jön létre, hogy rekurzívan meghívjuk ugyanezt az eljárás 1-gyel kisebb lépésszámmal, és harmadakkora szakaszhosszal, mint az előző lépésben.
Tehát az eljárás:
tanuld cantorpor :lépés :hossz
ha :n = 0 [előre :hossz]~
[cantorpor :lépés - 1 :hossz / 3~
tollatfel előre :hossz / 3~
tollatle cantorpor :lépés - 1 :hossz / 3]
vége
Ahhoz, hogy a teknőc ne függőlegesen felfelé rajzolja a Cantor-port, hanem vízszintesen, el kellene őt fordítani az elején 90 fokkal, a végén pedig vissza. Sajnos azonban ezt nem írhatjuk bele a cantorpor eljárásba, mivel a rekurzió miatt ez minden lépésben meghívódna, és a teknőc minden kis szakasz megrajzolása előtt forgolódna, ami furcsa eredményre vezetne (próbáld ki!). Ezért írunk egy főeljárást, melynek segítségével elfordítjuk a teknőcöt, majd meghívjuk a rekurzív eljárásunkat, a végén pedig visszafordítjuk a teknőcöt:
tanuld főcantor :lépés :hossz
jobbra 90
cantorpor :lépés :hossz
balra 90
vége
KOCH-GÖRBE
Ezt a fraktálszerű görbét Helge von Koch svéd matematikus 1906-ban írta le először. A Koch-görbe előállítási ötlete hasonló a Cantor-poréhoz, itt is minden lépésben kicseréljük a meglévő szakaszokat valami másra. Előállítási lépései a következők:
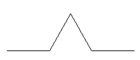
0. lépés: vegyünk egy szakaszt
1. lépés: a középső egyharmadát vágjuk ki, és emeljünk helyette "sátrat" két egyharmad hosszú szakaszból, mintha azok egy szabályos háromszög két oldalát alkotnák
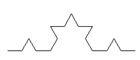
2. lépés: a keletkezett négy szakasszal tegyük ugyanezt
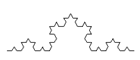
3. lépés: a keletkezett összes szakasszal tegyük ugyanezt
És így tovább. Amit végtelen lépés után kapnánk, az a Koch-görbe.

|
|
|
|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés |
| ... |
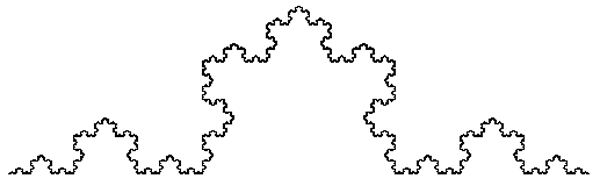
|
| 8. lépés |
Tehát az ötlet hasonló az előzőhöz: a 0. lépésben a teknőcnek egy folytonos szakaszt kell rajzolnia, a továbbiakban pedig minden szakasz helyett egy "sátras" szakaszt, mely 4 darab kisebb szakaszból áll, melyek hossza az előző lépésben szereplő szakasz egyharmada. Természetesen ezt is rekurzióval végezzük majd, a két paraméter pedig ugyanúgy a lépésszám és a szakaszhossz.
Az eljárás tehát:
tanuld koch :lépés :hossz
ha :lépés = 0 [előre :hossz]~
[koch :lépés - 1 :hossz / 3 balra 60~
koch :lépés - 1 :hossz / 3 jobbra 120~
koch :lépés - 1 :hossz / 3 balra 60~
koch :lépés - 1 :hossz / 3]
vége
Ez az eljárás azonban megintcsak függőlegesen felfelé rajzol. Tehát ismét szükségünk van egy főeljárásra, mely a teknőcöt irányba állítja, majd rajzoltat vele egy Koch-görbét, és visszaállítja őt a kezdőirányba:
tanuld főkoch :lépés :hossz
jobbra 90
koch :lépés :hossz
balra 90
vége
KOCH-HÓPEHELY
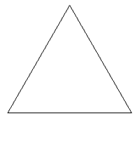
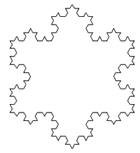
A Koch-hópehely vagy másnéven Koch-sziget három darab Koch-görbéből áll, melyek szabályos háromszög-alakban kapcsolódnak egymáshoz. Tehát az előző koch eljárást felhasználva Te is könnyedén megírhatod azt a kochpehely eljárást, melynek két paramétere ugyancsak a :lépés és a :hossz, és megrajzoltatja a három darab görbét a megfelelő szöggel elfordulva közöttük. Íme az eredmény:
|

|

|
|
| kochpehely 0 200 | kochpehely 1 200 | kochpehely 2 200 | kochpehely 3 200 |
SIERPINSKI-HÁROMSZÖG
Ezt a fraktált 1916-ban mutatta be Waclaw Sierpinski lengyel matematikus. A Sierpinski-háromszög az eddigiekkel ellentétben nem egy fraktálgörbe, hanem olyan fraktál, melynek előállításakor szakasz helyett egy egyszerű síkidomból, egy szabályos háromszögből kell kiindulnunk. Az előállítási szabály ezúttal sem bonyolult:
0. lépés: vegyünk egy szabályos háromszöglapot
1. lépés: kössük össze a háromszög oldalainak felezőpontjait egymással, így a háromszöget négy kisebb háromszögre osztottuk. A középső, csúcsára állított háromszöget vágjuk ki.
2. lépés: a maradék három kis háromszögnek ugyanígy vágjuk ki a közepét.
3. lépés: a keletkezett összes háromszöggel tegyük ugyanezt.
És így tovább. Amit végtelen lépés után kapnánk, az a Sierpinski-háromszög.

|

|

|

|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés |
| ... |

|
| 6. lépés |
LOGO-ban ez az eljárás kicsit bonyolultabb, mint az eddigiek. Az alapötlet az, hogy rajzo-unk egy fekete háromszöget, majd írunk egy rekurzív eljárást, mely egy-egy háromszög közepébe rajzol egy fehér, fejjel lefelé álló háromszöget. Ezen kívül lesz egy segédeljárásunk, mely egy adott színű háromszöget tud rajzolni.
Lássuk először ezt a segédeljárást. Nem tesz mást, mint rajzol egy szabályos háromszöget, és kiszínezi azt. A színezéshez felemelt tollal kell bemennünk a háromszög belsejébe, majd a színezés után visszatérni a háromszög sarkába.
tanuld háromszög :hossz :szín
ismétlés 3 [előre :hossz jobbra 120]
töltőszín! :szín tollatfel jobbra 30 előre 3
tölt hátra 3 balra 30 tollatle
vége
Most nézzük azt eljárást, mely egyetlen fehér, fejjel lefelé álló háromszög megrajzolásáért felelős. Hatására a teknőc a nagy háromszög bal alsó sarkából indulva, a tollat felemelve elmegy az alap feléig, ott helyes irányba fordul, majd alsó csúcsától kezdve felfelé megrajzolja a fehér háromszöget, végül a tollat felemelve visszamegy a nagy háromszög bal alsó csúcsába:
tanuld kivágháromszög :kishossz
tollatfel jobbra 90 előre :kishossz balra 120 tollatle
háromszög :kishossz 15
tollatfel balra 60 előre :kishossz jobbra 90
vége
A háromszög eljárással fehér színű háromszöget szeretnénk rajzoltatni, ezért az eljárásnak paraméterként a 15-öt adjuk, mely a fehér szín kódja.
Most már jöhet az igazi rekurzív eljárás, mely minden szükséges fehér háromszöget megrajzol (egy-egy lépésben összesen hármat):
tanuld sierpháromszög :lépés :hossz
ha :lépés > 0 [kivágháromszög :hossz~
ismétlés 3 [sierpháromszög :lépés - 1 :hossz / 2 ~
tollatfel balra 90 hátra :hossz * 2 tollatle balra 30]]
vége
Nincs más teendőnk, minthogy megírjuk a főeljárást, mely rajzol egy nagy fekete háromszöget, majd meghívja a fehér háromszögeket rajzoló eljárást (a tollszínt először feketére, majd fehérre, majd újból feketére váltja, hogy a háromszögek körvonalai is megfelelő színűek legyenek.):
tanuld fősierpháromszög :lépés :hossz
tollszín! 0 jobbra 30 háromszög :hossz*2 0 balra 30
tollszín! 15 sierpháromszög :lépés :hossz
tollszín! 0
vége
SIERPINSKI-SZŐNYEG
A Sierpinski-szőnyeg szintén síkbeli fraktál, előállítási ötlete ugyanaz, mint a Sierpinski-háromszögé, de mivel megrajzolása több ismétlést és rekurziót igényel, a részletes eljárásokat nem ismertetjük. Bemutatjuk viszont az előállítás szabályát, és az első néhány lépés után a fraktál kinézetét. Az előállítás lépései:
0. lépés: vegyünk egy négyzetet
1. lépés: kössük össze a négyzet oldalainak harmadolópontjait a szemközti harmadolópontokkal, így a négyzetet kilenc kisebb négyzetre osztottuk. A középső négyzetet vágjuk ki.
2. lépés: a maradék nyolc négyzetnek ugyanígy vágjuk ki a közepét.
3. lépés: a keletkezett összes négyzettel tegyük ugyanezt.
És így tovább. Amit végtelen lépés után kapnánk, az a Sierpinski-szőnyeg.

|

|

|

|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés |
BEKÜLDENDŐ FELADATOK
1. FELADAT
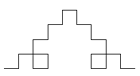
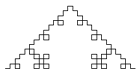
A leckében szereplő Koch-görbe előállítási ötlete alapján olyan fraktálokat is kitalálhatunk, melyek nem fűződnek híres matematikusok nevéhez. Az alábbi fraktál leginkább hímzett terítőre hasonlít, mégis könnyen megrajzolhatod az ábrák alapján. Az előállítás szabályát az alábbi ábrákról kell leolvasnod. Az 1. lépés árulja el, hogy mire kell kicserélni minden lépésben a keletkezett szakaszokat.

|

|
|
|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés |
| ... |

|
| 7. lépés |
2. FELADAT
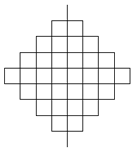
Ugyanezzel az ötlettel rajzolható meg a Peano-görbe is. Ezt az alakzatot Giuseppe Peano olasz matematikus jelentette meg először 1890-ben. Érdekessége, hogy a Peano-görbe egy úgynevezett térkitöltő görbe, ami azt jelenti, hogy bár egyetlen vonallal megrajzolható, végtelen lépés után mégis hézag nélkül kitöltené, "kiszínezné" a síkot. Ha megírod a Peano-görbét előállító eljárást LOGO-ban, már néhány lépés után is jól látszik, hogy tölt ki a görbe egy négyzetet. Jól figyeld meg az 1. lépés ábráját, vedd figyelembe, hogy tulajdonképpen 9 darab kis szakaszból áll!
|

|
|

|

|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés | 4. lépés |
3. FELADAT
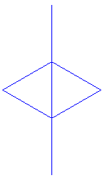
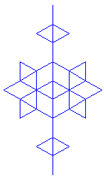
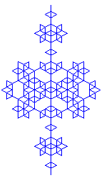
Most pedig "gyúrjuk össze" a Koch- és a Peano-görbét! Ezeket összekeverve egy lepkeszerű fraktált kapunk.
|
|
|
|

|

|
| 0. lépés | 1. lépés | 2. lépés | 3. lépés | 4. lépés | 5. lépés |
4. FELADAT
Találj ki saját fraktálokat is! Találj egy olyan alakzatot, amire a szakaszokat minden lépésben kicseréled! Legjobb, ha papíron megrajzolod az első 1-2 lépést, és utána írsz rá eljárást. Válaszd ki hozzá kedvenc tollszínedet!
| Vissza az oldal tetejére | Az érdekességekhez | ||
|---|---|---|---|
| Előző lecke | Következő lecke |