3. lecke - Mandalák

BEVEZETŐ - MIK AZOK A MANDALÁK?

A mandala eredetileg a buddhista valláshoz kapcsolódik. A szó a szanszkrit nyelvből ered, a mandala szanszkrit nyelven kör-t jelent. Hagyományosan kör alakú alapra festett, geometriai alakzatokból álló, középpontosan szimmetrikus színes képről van szó, melyet a buddhisták a meditáció, a mély gondolkodás egy formájaként festettek. Festés közben az alkotó megnyugszik, elfeledkezik gondjairól, és elgondolkodhat a világ folyásáról és saját magáról. Így a mandala egyszerre jelképezi az alkotót magát és az őt körülvevő világot, tükrözi alkotója lelkivilágát és a világhoz fűződő kapcsolatát.

Eredetileg tehát a kézzel festett mandalák minden egyes apró részletének külön jelentése volt. Manapság azonban sokan festenek vagy rajzolnak mandalát csak a szépsége miatt, mindenféle mögöttes jelentés nélkül. Mi is ezt fogjuk tenni, mégpedig a LOGO segítségével.

Hivatalos szabály tehát nem létezik arra, hogy mi is az a mandala. Általában viszont elmondhatjuk, hogy a mandala három legfontosabb tulajdonsága, hogy kör alapú, színes és középpontosan szimmetrikus legyen. Ennyit elég is tudni róla, kezdődhet a rajzolás!

HOGYAN RAJZOLJUNK LOGO-BAN MANDALÁT?

Mandaláink különböző apró, színes sokszögekből állnak majd, ezek a sokszögek mind egy-egy külön kis eljárást fognak jelenteni. A sokszögekből először felépítjük a mandala egy "szeletét", azután egy nagy körlapra ebből a szeletből körbe elhelyezünk annyit, amennyit csak szeretnénk. Majdnem úgy, mintha egy virágot rajzolnánk: először megrajzolunk egyetlen szirmot, aztán sokszor egymás mellé illesztjük ugyanazt a szirmot, amíg körbe nem érünk.

A sokszögek most egyik csúcsukon állnak majd, és ettől az alsó csúcstól kezdve rajzoljuk meg őket. Az egyes szeletek megrajzolása után pedig mindig vissza kell állni a szelet csúcsához, azaz a mandala közepéhez, hogy a következő szeletet is jó helyről kezdjük rajzolni.

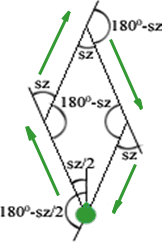
A mandalák gyakori díszítőeleme a rombusz, írjunk tehát először erre eljárást. A rombusz két paramétere az oldalhossz és az alsó és felső csúcsnál található szög lesz. Az ábra mutatja, hogy mikor miért annyit kell fordulni, amennyi az eljárásban szerepel. Az ábrán az eljárásban szereplő szög-et sz betűvel jelöltük, a teknőc útját a zöld nyilak jelölik.

tanuld rombusz :hossz :szög balra :szög / 2 előre :hossz jobbra :szög előre :hossz jobbra 180 - :szög előre :hossz jobbra :szög előre :hossz jobbra 180 - :szög / 2 vége

A díszítéshez bármilyen szabályos sokszöget is felhasználhatunk, úgyhogy írjunk egy olyan általános sokszög eljárást, amely csúcsára állított szabályos sokszöget rajzol, két paramétere pedig a csúcsok száma és az oldalhossz.

Ismétlésképpen nézzük meg, hogy nézett ki az általános sokszög eljárásunk:

Ezt az eljárást kell kiegészíteni azzal, hogy az elején forduljon el a teknőc a sokszög belső szögének felével, a végén pedig forduljon vissza (ugyanúgy, ahogy a rombusznál), így fog a sokszög a csúcsán állni. Kérdés, hogyan tudjuk kiszámolni a sokszög belső szögének felét?

Azt tudjuk, hogy a teknőcnek rajzolás közben annyit kell fordulnia, amennyi a külső szög, ez pedig 360°/n, ha n a sokszög csúcsainak száma. A belső szöget megkapjuk, ha 180°-ból kivonjuk a külső szöget, ez tehát 180°-360°/n. Ennek kell most a fele, ami tehát (180°-360°/n)/2, ami egyszerűsítve 90°-180°/n. Ennyit kell tehát a teknőcnek elfordulnia balra az eljárás kezdete előtt. Az átalakított eljárásunk tehát a következő:

Írjunk egy kiszínező eljárást is, amely egy csúcsára állított sokszöget kiszínez. Mindössze annyit kell tennie, hogy felemelt tollal előre küldi pár lépéssel a teknőcöt, színez, majd visszaáll eredeti helyére. Az eljárás paramétere a szín lesz, hogy milyenre színezzen, amit 0 és 15 közötti számmal tudunk majd megadni.

Vigyázat! Az eljárás mindig az első határvonalig színez, tehát nem fog jól működni, ha egymásba érő alakzatokat szeretnél kiszínezni, illetve túl apró alakzat esetén az egész képernyőt kiszínezheti. (Apró alakzatok esetén olyan színező eljárást használj, amely csak 2-3 lépést lép előre a színezéshez.)

Próbáld ki meglévő eljárásaidat az alábbiakhoz hasonló parancsokkal:

Színes körlapot pedig a már ismert pont parancs segítségével fogunk rajzolni, ahogyan a 2. leckében a koncentrikus köröket. A pont parancs használatánál arra kell csak figyelni, hogy előtte mindig jó nagyra kell állítani a tollvastagságot (attól függően, hogy mekkora kört szeretnénk rajzolni), utána azonban mindig állítsuk vissza 1-re, különben a további utasításokat is ezzel az elképesztő tollvastagsággal fogja végrehajtani.

Másranincs is szükségünk az egyszerűbb mandalákhoz. Az első próbálkozásunk legyen olyan mandala, melynek díszítéséhez nincs más sokszögre szükségünk, csak rombuszokra. Ennek egy szelete 4 darab rombuszból áll, a zöldből, két kékből és egy lilából. A rombuszok méretét és szögét, a köztük lévő távolságokat és a színeket próbálgatással határoztam meg. Így tehát az eljárás:

tanuld szelet1 tollszín! 2 rombusz 70 20 kitölt 2 tollatfel előre 150 tollatle tollszín! 5 rombusz 20 30 kitölt 5 tollatfel hátra 20 balra 90 előre 10 tollatle tollszín! 9 rombusz 30 150 kitölt 9 tollatfel jobbra 180 előre 20 tollatle tollszín! 9 rombusz 30 150 kitölt 9 tollatfel hátra 10 balra 90 hátra 130 tollatle vége

Most már nincs is más dolgunk, minthogy rajzoljunk egy nagy körlapot (pontot), majd arra az ismétlés paranccsal körben sok ilyen szeletet. Ahhoz, hogy körbeérjünk a szeletekkel, ugyanazt a módszert kell alkalmaznunk, mint az 1. leckében a sokszögmintáknál, azaz az ismétlések száma szorozva a fordulási szöggel legyen mindig 360°. Az ábrán látható mandala megrajzolásához például 12 szeletet használtam fel, így két szelet megrajzolása között 30°-ot kell elfordulni:

Próbáld ki a mandala1 parancsot! Ugye, ugyanazt kapod, mint ami az ábrán látható?

Természetesen a színeket tetszőlegesen választhatod meg, bármilyen 0 és 15 közötti számot írhatsz a tollszín! és kitölt parancsok után. Sőt, az eljárásokat átírhatjuk úgy is, hogy a színeket paraméterekként lehessen megadni. Ekkor az eljárások így módosulnak:

Így az előző mandalát a mandala1param 2 5 9 11 paranccsal rajzolhatod meg, de más számokkal természetesen ugyanilyen mintájú, de más színű mandalákat kapsz. Az eljárást meghívhatod véletlenszámokkal is, ahogyan azt az 1. leckében a sokszögmintákkal tettük. Most négy darab színt kell paraméterként megadni, mind a négy helyett írhatunk véletlenszám 16-ot.

Tehát a mandala1param véletlenszám 16 véletlenszám 16 véletlenszám 16 véletlenszám 16 parancs akárhányszor meghívod, annyiszor más színű mandalát rajzol. Én ilyen mandalákat rajzoltam ezzel a paranccsal:

És Te?

Természetesen nem csak a színeket változtathatod, hanem például azt is, hogy hány szelettel díszíted a mandalát. Ehhez a mandala1 eljárásban kell átírni az ismétlések számát és az elfordulás szögét.

	A szeletek lehetnek ritkábban,...		...vagy sűrűbben.

Látod, mennyit lehet játszani egyetlen fajta mintázattal? Most lássunk egy másik mintát is. Ezen a mandalán már nemcsak rombuszok vannak, hanem kisebb körök is. Ráadásul a rombuszok nem pont a mandala közepén kezdődnek, hanem kicsit előrébb, hogy a középső pötty is elférjen. Ennek a mandalának egy szelete egy bordó rombuszból és tőle jobbra egy zöld pöttyből áll. A nagy, sárga kört és a középső világoskéket a külső, mandala2 eljárásban rajzoljuk majd meg.

Tehát a szelet: tanuld szelet2 tollatfel előre 50 tollatle tollszín! 4 rombusz 80 30 kitölt 4 tollatfel előre 120 jobbra 90 előre 30 tollatle tollszín! 2 tollvastagság! 20 pont tollvastagság! 1 tollatfel hátra 30 balra 90 hátra 170 tollatle vége

Ebből a szeletből teszünk majd egymás mellé 18-at, 20°-os elfordulási szöggel, miután megrajzoltuk a nagy sárga, és a kisebb világoskék kört:

Ennek a mandalának is sokat lehet játszani a színeivel. Ha a szeletek sűrűségével játszol, nem lesz szimmetrikus a minta, mivel egy-egy szelet sem szimmetrikus. Ha több vagy kevesebb szeletet használsz, a köztük lévő zöld pöttyök nem fognak középen látszani.

Tudsz hasonlókat?

A következő mandala mintázata egy kicsit több sokszögből áll. Láthatsz rombuszokat, valamint pöttyöket, körülöttük apró háromszögekkel. Az alap pedig két körlap (egy világoskék és egy lila) egymásra rajzolva. Mivel a sárga pöttyöket sok kis piros háromszöggel maga körül nagyon sokszor felhasználtam a mandalához, erre a mintarészletre külön eljárást írtam. Az eljárást kisvirágnak neveztem el:

tanuld kisvirág tollszín! 14 tollvastagság! 30 pont tollvastagság! 1 ismétlés 12 [tollatfel előre 20 tollszín! 4~ tollatle csúcssoksz 3 10 kitölt 4~ tollatfel hátra 20 jobbra 30 tollatle] vége

Ezzel az eljárással már könnyen megírhatjuk a mandala egy szeletének eljárását: tanuld szelet3 tf előre 40 tl tollszín! 2 rombusz 60 30 kitölt 2 tf előre 150 tl kisvirág tf hátra 190 tl vége

Magához a mandalához pedig rajzolnunk kell két körlapot, majd középre egy kisvirágot, és az előbbi szeletből 20-at egymás mellé, 18°-os elfordulási szöggel.

Próbáld ki, milyen mandalákat kapsz, ha megváltoztatod a színeit és a szeletek sűrűségét!

1. FELADAT

Rajzold meg az ábrán látható mandalát! A kisebb, ismétlődő mintázatokra írj külön-külön eljárásokat! Ahhoz, hogy minden kicsi minta a mandala közepe felé nézzen, két minta megrajzolása között mindig vissza kell hátrálni a mandala közepéig, majd elfordulva az új minta helyére menni.

2. FELADAT

Rajzold meg az ábrán látható mandalát! A kisebb, ismétlődő mintázatokra írj külön-külön eljárásokat! Vigyázz! Az egymásra rajzolt, vagy túl kicsi alakzatoknál lehet, hogy trükközni kell a színezéssel!

3. FELADAT

Rajzold meg az ábrán látható mandalát! A kisebb, ismétlődő mintázatokra írj külön-külön eljárásokat! Vigyázz! A túl kicsi alakzatoknál nem biztos, hogy a színezés tökéletes lesz! A hullámvonalat egyetlen hullámhegy-hullámvölgy párosból raktam össze ismétléssel és forgatással. Addig próbálgattam a távolságokat, míg a kis hullámok pontosan össze nem értek.

4. FELADAT

Rajzolj saját mandalákat! Tartalmazzon minél több alakzatot, legyen színes, és mindenképpen középpontosan szimmetrikus!

	Vissza az oldal tetejére		Az érdekességekhez
	Előző lecke		Következő lecke