5. lecke |
6. lecke |
7. lecke |
8. lecke |
9. lecke |
|---|

4. lecke - Körök és körívek
 |
 |
 |
KÖR RAJZOLÁSA SOKSZÖGKÉNT
Ebben a leckében sok-sok színes kört, körívet és ezekből álló képeket fogunk rajzolni. Teknőcünk magától nem ismer semmiféle kör-rajzoló eljárást, így nekünk kell azt megírni. Ez nem is nehéz, hogyha csalunk egy kicsit. Emlékezzünk csak vissza a sokszögekre, amiket az első leckében rajzoltunk! Hogy is volt a sokszöget rajzoló eljárásunk? Valahogy így:
tanuld soksz :hossz :szögszám
ismétlés :szögszám [előre :hossz jobbra 360/:szögszám]
vége
Ezzel az eljárással bármilyen sokszöget meg tudunk rajzolni, csak meg kell adni az oldalhosszát, és hogy hány szöge (azaz csúcsa) legyen. Az első leckében már kipróbáltuk, mit kapunk az alábbi parancsokkal, de nézzük meg még egyszer!
soksz 100 6
soksz 50 12
soksz 30 36
soksz 20 72
Látszik, hogy minél több csúcsa van egy sokszögnek, annál jobban hasonlít egy körhöz. Tehát, ha kört szeretnénk rajzolni, nincs is más dolgunk, minthogy egy lehető legtöbb csúccsal rendelkező sokszöget rajzoljunk! Az első leckében az is kiderült, hogy az eljárás során a teknőc akkor szöggel fordul minden lépésben, hogy ez a szög megszorozva a csúcsok számával pontosan 360 legyen.
Azaz, ha például minden lépésben csak egyetlen fokkal fordulna el, akkor a sokszögnek 360 csúcsa kellene, hogy legyen ahhoz, hogy a teknőc körbeérjen, és a sokszög bezáruljon. Próbáljuk ki tehát, hogy néz ki a 360-szög!
soksz 1 360
Ugye egészen úgy néz ki, mint egy kör? Ezek alapján meg is írhatjuk első kör-eljárásunkat: nincs más dolgunk, mint 360-szor egymás után előre menni egy lépést és jobbra fordulni egy fokot.
|
tanuld kör1 |
 |
Ezzel azonban mindig csak ugyanakkora köröket tudunk rajzolni, hiszen a lépéshosszt 1-nek adtuk meg. Már a sokszögeknél is láttuk azonban, hogy nem nehéz paraméterként megadni a lépéshosszt, és így az eljárás meghívásakor dönthetjük el, hogy mekkora kört szeretnénk rajzolni. Ugyanúgy kell tenni, mint a soksz eljárás esetén, ahol két paraméterünk is volt, de most elég csak egy, a hossz.
tanuld kör2 :hossz
ismétlés 360 [előre :hossz jobbra 1]
vége
Így már aztán akármekkora köröket tudunk rajzolni! Próbáld ki!
kör2 1
kör2 2
kör2 3
Sőt, akár törtszámokkal is meghívhatjuk az eljárást. Kipróbálhatod tehát akár így is:
kör2 0,8
kör2 2,5
kör2 3,3
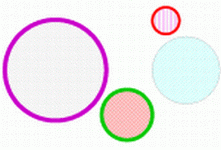
SZÍNES, MINTÁS KÖRÖK
|
És ezt a kört hogy rajzoltam? |
 |
Mit kell tennünk ahhoz, hogy ilyen érdekes, színes és mintás köröket tudjunk rajzolni? Változtassuk meg a tollszínt, tollvastagságot, válasszunk kitöltőszínt és kitöltőmintát! Ezekkel már mind találkoztunk korábban, most csak ki kell bővítenünk már meglévő eljárásunkat a megfelelő parancsokkal. Ezeket az adatokat mind paraméterként fogjuk megadni azért, hogy különböző köröket rajzolhassunk. Tehát a hossz-on kívül lesz még egy vastagság, vonalszín, minta és töltszín paraméterünk is.
Tehát az eljárás a következő:
tanuld kör3 :hossz :vastagság :vonalszín :minta :töltszín
tollszín! :vonalszín
tollvastagság! :vastagság
töltőminta! :minta
töltőszín! :töltszín
ismétlés 360 [előre :hossz jobbra 1]
tollatfel jobbra 90 előre :vastagság + 5
tölt
hátra :vastagság + 5 balra 90 tollatle
tollszín! 0
tollvastagság! 1
töltőminta! 0
töltőszín! 0
vége
Az eljárás elején beállítjuk az összes szükséges színt és mintát, majd megrajzoljuk a kört, utána pedig a kitöltés következik:
tollatfel jobbra 90 előre :vastagság + 5: ez azt jelenti, hogy a kör megrajzolásának befejezése után jobbra fordulunk és bemegyünk a körön belülre, hiszen csak így lehet majd kiszínezni a kört. Előtte persze fel kell emelni a tollat, hogy ne húzzunk vonalat a kör belsejébe. A tollvastagságnál 5-tel nagyobb lépést teszünk befelé, hogy biztosan ne a kör vonalán álljunk meg, mert akkor a vonalat fogjuk kiszínezni, és nem a kör belsejét.
tölt: kiszínezzük a kört.
hátra :vastagság + 5 balra 90 tollatle: visszamegyünk a körvonalra, visszafordulunk menetirányba, és letesszük a tollat, hogy pontosan ugyanott és ugyanúgy fejezzük be az egész kör megrajzolását, ahogyan elkezdtük. Ugyanezért állítjuk vissza az eljárás legvégén a színeket és tollvastagságot is az eredetire.
Ezentúl a tollatfel és tollatle parancsok rövidítéseit fogjuk használni: tf és tl.
Ne feledjük, hogy a lépéshosszon kívül a színeket is számok segítségével kell megadnunk (a színeket 0 és 15, a mintát 0 és 6 közötti számmal adhatjuk meg). Vagyis az eljárást például a következőképpen hívhatjuk meg:
kör3 2 3 5 4 7
Ezt az eljárást felhasználva rajzolhatnánk egy pöttyös labdát például. Ehhez egy nagy piros kör kell, majd arra több kisebb fehér, a pöttyöknek. Ezek a körök nem mintásak, hanem egységesen vannak kitöltve, ezért a mintának 0-t kell választanunk, ez jelenti a teli kitöltést.
|
tanuld labda |
 |
KÖRÖK VÉLETLENSZERŰ SZÍNNEL ÉS MINTÁVAL
Természetesen, ha nincs kedvünk olyan sok paramétert megadni minden egyes kör rajzolásakor, mint a kör3 eljárás esetén, és nincs konkrét ötletünk, milyen kört szeretnénk rajzolni, akkor a véletlenre is bízhatjuk a vonalvastagság, a színek és a minta megválasztását. A véletlenszámokat használó eljárásokban az a jó, hogy ha ugyanúgy hívjuk is meg őket, mindig mást rajzolnak. Ehhez az eljárásban ki kell cserélni azokat a részeket, amelyek ezeket az adatokat állítják be, és a paraméterek helyett a véletlenszám parancsot kell használni:
|
tanuld kör4 :hossz |
 |
Néhány sorát ennek a hosszú eljárásnak jobb, ha kiemeljük, és külön megvizsgáljuk:
tollvastagság! ( 1 + véletlenszám 15 ): a tollvastagságra 1 és 15 közötti számot szeretnénk beállítani. A véletlenszám 15 parancs azonban 0 és 14 közötti számot választ. Ha azonban a választott számhoz hozzáadunk 1-et, akkor biztosan 1 és 15 közötti számot kapunk.
tf jobbra 90 előre :hossz * 10: ez a sor is megváltozott az előző eljáráshoz képest, hiszen most nem tudjuk, mennyi lesz a vonalvastagság, nem használhatjuk fel ezt az adatot. A cél azonban most is az, hogy bejussunk a kör belsejébe, ahol kiadhatjuk a tölt parancsot. Nem számít, pontosan mennyit megyünk, a lényeg, hogy bejussunk a kör belsejébe. Most a lépéshossz 10-szeresét lépjük le előre, hogy beérjünk a körbe, majd a színezés után ugyanennyit megyünk vissza.
Most pihenésképpen használjuk ki legújabb eljárásunkat, és állítsunk össze egy valóságos műalkotást véletlenszerűen rajzolt körökből, például így:
|
tanuld körök |
  |
Ezt a körök eljárást akárhányszor hívod meg, mindannyiszor más-más műalkotást fog rajzolni.
KÖRÍVEK
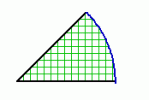
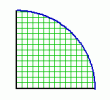
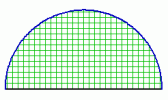
Most pedig egy kicsit hagyjuk a köröket, és térjünk át a körívekre. Most tehát a körvonalaknak csak egy-egy darabkáját fogjuk megrajzolni. Egy körív mérete két dologtól függ: attól, hogy mekkora körnek a darabja (ezt az eddig is használt lépéshossz határozza meg), és hogy mekkora darabot vágunk ki a körből. Ezt pedig egy szög megadásával lehet meghatározni, mégpedig úgy, hogy a körív két végét össze kell kötni (akár képzeletben) annak a körnek a középpontjával, melynek darabjai. A két összekötő vonal bezár egy szöget, ez határozza meg, hogy mekkora a körív. Minél nagyobb a szög, annál hosszabb a körív, ahogy az alábbi ábrákon is láthatod:
 |
 |
 |
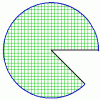 |
| Itt a szög 45°-os | Itt a szög 90°-os | Itt a szög 180°-os | Itt a szög 315°-os |
Eddig, amikor kört rajzoltunk, a kör eljárásban 360-szor kellett ismételnünk az egy egységnyit előre lépést és egy fokot fordulást, így értünk pont körbe. A teljes kör felfogható egy 360°-os körívnek is. Ebből láthatjuk, hogy körív rajzolása esetén annyi ismétlést kell alkalmaznunk, amennyi a körív szöge. Az eljárásunkban tehát a két paraméter legyen szög és hossz.
|
tanuld körív :szög :hossz |
 |
| körív 60 5 |
Körívekből is alkothatunk érdekes műalkotásokat, például ha többfajta körívet összekötünk a végüknél fogva. A körívek legyenek különböző színűek és méretűek (a véletlenszám parancs segítségével határozzuk meg), és az összekötő pontoknál véletlenszerűen forduljunk mondjuk jobbra valahány fokot.
|
tanuld körívek :db |
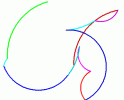 |
Látszik, hogy az eljárásnak egyetlen paramétere van, mégpedig, hogy hány darab körívet szeretnénk összekapcsolni. Az összes többi adatot véletlenszámok segítségével határozzuk meg.
Az eljárás néhány parancsát vizsgáljuk meg kicsit közelebbről:
körív véletlenszám 180 ( 1 + véletlenszám 3 ): a körív eljárást hívjuk meg, melynek két paramétere a szog és a hossz. A szöget itt a véletlenszám 180 parancs határozza meg, mely egy 0 és 179 közötti számot eredményez. A hosszt az 1 + véletlenszám 3 parancs határozza meg, mely egy 1 és 3 közötti számot ad eredményül. A zárójelek csak arra valók, hogy a két paramétert elválasszák egymástól.
jobbra véletlenszám 360: tetszőleges (0 és 359 fok közötti) szöggel fordul jobbra.
Most már akár úgy is rajzolhatunk teljes kört, hogy tetszőleges számú, egyforma hosszú körívből rakjuk össze. Ahhoz, hogy látszódjanak a körívek határa, minden körív legyen más színű! Olyan eljárást írunk, ahol az egyetlen paraméter azt fogja megadni, hogy a kör hány körívből álljon (ez lesz a db), és természetesen most is a körív eljárást használjuk fel.
|
tanuld kör_ívekből :db |
 |
Próbáld ki!
kör_ívekből 3
kör_ívekből 6
kör_ívekből 10
Látod? Amennyi a paraméter, annyi körívből fog állni a kör.
Mi is történt valójában? A körvonalat fel kell osztanunk annyi darab körívre, ahányat a db paraméter megad nekünk. De hogyan? A körívnek két paramétere van, az egyik a szog, a másik a hossz. A szog pontosan azt mutatja meg, hogy a körív mekkora része legyen a teljes körnek. Ahány körívet szeretnénk, annyi részre kell osztanunk a teljes kört, vagyis a 360°-ot. Ezért a körív szöge 360 / :db, ez az első paraméter. A második paramétertől csak az függ, hogy mekkora kört kapunk a végén. Ez tehát szabadon választott, a fenti példában éppen 3-at írtunk, de lehet bármi (ha túl nagy számot választunk, a kör nem fog kiférni a képernyőre).
Tehát a körív ( 360 / :db ) 3 parancs első paramétere a ( 360 / :db ), mely a szöget határozza meg, második pedig 3, mely a leendő kör nagyságát határozza meg.
KITÉRŐ - A Π bevezetése
Az eddigiekben mindig csak úgy tudtunk kört vagy körívet rajzolni, hogy a körív egy pontjából indultunk, és ugyanoda is érkeztünk vissza. Sokszor azonban kényelmesebb lenne, ha a kör középpontjából tudnánk megrajzolni a kört vagy körívet, és ugyanoda érnénk vissza. Eddig, ha a középpontból rajzoltunk kitöltött kört, akkor a pont parancsot használtuk (a 2. leckében a koncentrikus köröknél, vagy a 3. leckében a mandaláknál), a pont parancs segítségével azonban csak színes körlapot tudunk rajzolni, nem pedig körvonalat vagy körívet.
Ezért új ismeretekre van szükségünk. Olyan eljárás kellene, melyben a kör középpontjában álló teknőcnek csak a kör sugarát kellene megadnunk, és megrajzolná a kört. A teknőcnek pontosan a kör kerülete mentén kell végigsétálnia vonalat húzva maga után. Tehát, ha tudni akarjuk, mennyit kell előre mennie, tulajdonképpen az a kérdés, hogyan tudjuk kiszámolni a kör kerületét a sugara alapján.
Megpróbáljuk mérések alapján kitalálni a választ. Fogj egy papírt, egy körzőt és egy cérnaszálat a kísérlethez! Rajzolj a papírra a körzővel 0,5 cm, 1 cm, 2 cm, 3 cm és 5 cm sugarú kört! Mérd meg a kerületüket úgy, hogy a cérnaszálat minél pontosabban megpróbálod az egyes körök kerületére illeszteni, bejelölöd a pontot, ahol összeér a cérnaszál, majd leveszed a körről, a vonalzóra illeszted, és ott megméred a bejelölt cérnaszál hosszát.
Ennek alapján az alábbi táblázatot írhatjuk fel. Te is hasonló adatokat kaptál a kerületre? Természetesen a mérés nem lehet egészen pontos, de ha ügyesen mértél, Te is hasonló számokat kaptál.
| Sugár (r) | 0,5 cm | 1 cm | 2 cm | 3 cm | 5 cm |
| Átmérő (d) | 1 cm | 2 cm | 4 cm | 6 cm | 10 cm |
| Kerület (k) ~ | 3,14 cm | 6,28 cm | 12,56 cm | 18,84 cm | 31,4 cm |
Ha figyelmesen megnézzük az átmérő és a kerület mérőszámait, észrevehetjük, hogy szoros kapcsolat áll fenn közöttük. Az átmérőt minden esetben 3,14-dal megszorozva kapjuk meg a kerületet. Ez egy nevezetes szám, pi-nek hívják. A pi egy görög betű, a görög "kerület" szó ezzel a betűvel kezdődik, és így írják: Π. A Π szám igazából egy végtelen tizedestört, 50 tizedesjegy pontossággal így néz ki: 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510. Amikor számolunk vele, általában 3,14-nek szoktuk kerekíteni.
Most már tehát felírhatjuk, hogy tudjuk kiszámolni a kör kerületét az átmérője (d) illetve a sugara (r) segítségével: k=dΠ vagy k=2rΠ. A további rajzokhoz ezt az összefüggést fogjuk használni.
KÖRÖK RAJZOLÁSA A SUGÁR MEGADÁSÁVAL
Ezek után nézzük, hogyan rajzolhatunk kört és körívet úgy, hogy csak a sugarat adjuk meg paraméterként.
Most már tudjuk, hogy ha a kör sugara r, akkor a kerülete 2rΠ, vagyis a teknőcnek egy teljes kör rajzolása esetén 2rΠ hosszú vonalat kell húznia. A teknőc eddig úgy rajzolt kört, hogy 360-szor ismételve előre ment valamennyit, majd jobbra fordult 1°-ot. Az a kérdés, hogy ha adott a sugár, vagyis a kör mérete, akkor honnan tudjuk, hogy egy-egy lépésben mennyit kell a teknőcnek előre mennie? Nos, a válasz kitalálható: ha 360 lépés alatt 2rΠ-t megy előre, akkor 1 lépés alatt 2rΠ/360-at, vagyis kerekítve 2r*3,14/360-at. A 2r*3,14/360 pedig egyszerűsíthető úgy, hogy a 2r*3,14-t és a 360-at is elosztjuk 2-vel, így az eredmény: r*3,14/180, vagy 3,14*r/180.
Tehát az új eljárás:
tanuld kör5 :sugár
ismétlés 360 [előre 3,14 * :sugár / 180 jobbra 1]
vége
Próbáld ki!
kör5 50
kör5 100
kör5 200
KÖR RAJZOLÁSA A KÖR KÖZEPÉBŐL KIINDULVA
Még elegánsabb lenne az eljárásunk, ha a rajzolást nem a kör vonaláról, hanem a kör középpontjából kezdhetnénk. Így ugyanis sokszor egyszerűbb pontosan elhelyezni a köröket. Ehhez nem sokkal kell kiegészítenünk az eljárást, csak annyival, hogy rajzolás előtt a teknőcöt felemelt tollal el kell küldeni a kör középpontjából a körvonalra, ami pontosan sugárnyi távolság. Ezután irányba állítjuk, az előbb tanult módon megrajzoltatjuk vele a kört, majd felemelt tollal visszaküldjük a kör közepére. Lássuk az eljárást:
tanuld kör6 :sugár
tollatfel balra 90 előre :sugár jobbra 90 tollatle
ismétlés 360 [előre 3,14 * :sugár / 180 jobbra 1]
tollatfel jobbra 90 előre :sugár balra 90 tollatle
vége
Látszik, hogy maga a kör megrajzolása nem változott a kör5 eljáráshoz képest, azaz ezt is írhattam volna:
tanuld kör6 :sugár
tollatfel balra 90 előre :sugár jobbra 90 tollatle
kör5 :sugár
tollatfel jobbra 90 előre :sugár balra 90 tollatle
vége
Így a kitöltés sokkal egyszerűbb lett, hiszen az eljárás végén a kör közepén állunk, ahol nyugodtan kiadhatjuk a tölt parancsot. Rajzoljunk színes körlapot úgy, hogy a színt paraméterként adjuk meg!
|
tanuld körlap :sugár :szín |
 |
Ez az eljárás pontosan helyettesíti a pont parancsot.
Így akár már gyönyörű céltáblát, azaz koncentrikus köröket is rajzolhatunk!
körlap 200 0
körlap 150 15
körlap 100 0
körlap 50 15
SZÍNES KÖRÖK RAJZOLÁSA A SUGÁR MEGADÁSÁVAL
Kibővíthetnénk úgy is, hogy a mintát is meg lehessen adni paraméterként.
|
tanuld körlap2 :sugár :szín :minta |
 |
Ha pedig szeretnénk, átírhatnánk úgy is az eljárást, hogy a paramétereket a véletlenszám parancs határozza meg, és ne nekünk kelljen megadni.
Ennek segítségével egyszerűen tudunk például körgyűrűt rajzolni: rajzoljunk egy színes körlapot, és rajzoljunk rá egy kisebb, fehér körlapot!
|
tanuld körgyűrű |
 |
Sőt, a 2. lecke koncentrikus köreit is előállíthatjuk most már úgy, hogy pont parancs helyett a saját körlap eljárásainkat használjuk.
|
Ha pedig a körlap és a körlap2 eljárásokat felváltva használjuk, akkor ilyen félig mintás körlapot is rajzolhatunk. |
 |
Tudunk teljesen mintás körlapokat is rajzolni egymásra? Próbáld ki!
KÖRÍVEK RAJZOLÁSA A SUGÁR MEGADÁSÁVAL
Nézzük most mindezeket körívek esetén. Körívek rajzolásánál annyi volt a különbség a körhöz képest, hogy nem 360-szor ismételtük az előremenést és fordulást, hanem annyiszor, amennyi a körív szöge volt. Így természetesen két paraméterre lesz szükségünk: a sugáron kívül meg kell adnunk a körív szögét is.
Így az új eljárás:
tanuld körív2 :sugár :szög
ismétlés :szög [előre 3,14 * :sugár / 180 jobbra 1]
vége
Két ilyen körív segítségével könnyedén rajzolhatunk egy virágszirmot:
|
tanuld szirom :sugár :szög |
 szirom 150 75 |
Lássuk, hogyan lesz a szirmokból virág! Paraméterként megadjuk a szirmok sugarát és darabszámát.
|
tanuld virág :sugár :szög :sziromdb |
 virág 100 60 20 |
(Ha színes virágot szeretnénk, a rajzolás előtt be kell állítani a tollszínt.)
Mi is történt valójában? Az 1. leckében rajzolt sokszögmintákhoz hasonlóan gondolkodunk: megrajzolunk egy szirmot, majd elfordulunk egy kicsit, és megrajzoljuk a következőt, addig, amíg körbe nem érünk. Ahhoz, hogy pontosan körbeérjünk, és annyi szirmunk legyen, amennyit megadunk, ahhoz a sziromrajzolást és fordulást sziromdb-szor kell ismételni, és a szirmok megrajzolása között 360/sziromdb-nyit fordulni.
Bővítsük ki a szirom eljárást úgy, hogy a szirom körvonalának és belsejének színét is paraméterként lehessen megadni!
|
tanuld szirom2 :sugár :szög :szín |
 szirom2 150 75 1 |
Nem történik más, mint beállítjuk a színeket, az előző eljárás alapján megrajzoljuk a szirmot, majd bemegyünk a belsejébe, kiszínezzük, visszamegyünk a kiindulópontba, és visszaállítjuk a színeket.
Lássuk, hogyan lesz igazán színes virágunk!
tanuld virág2 :sugár :szög :sziromdb :szín
ismétlés :sziromdb [szirom2 :sugár :szög :szín~
jobbra 360 / :sziromdb]
vége
Te is tudsz ilyeneket rajzolni? (Túl sok szirom esetén gond lehet a színezéssel.)
 |
 |
 |
 |
KÖRÍV RAJZOLÁSA A KÖR KÖZEPÉBŐL KIINDULVA
Érdemes olyan eljárást is írnunk, mely a kör közepéből indulva rajzol körívet:
tanuld körív3 :sugár :szög
tollatfel balra 90 előre :sugár jobbra 90 tollatle
ismétlés :szög [előre 3,14 * :sugár / 180 jobbra 1]
tollatfel jobbra 90 előre :sugár balra 90 tollatle
balra :szög
vége
Utolsó utasításként azért szükséges a balra :szög utasítás, mert a teknőc most nem teljes kört fordul, csak egy bizonyos szögnyit, és ha azt szeretnénk, hogy a rajzolás végeztével orra ugyanarra mutasson, mint induláskor, akkor ugyanezzel a szöggel vissza kell fordítani őt.
Próbáld ki!
körív3 100 30
körív3 100 90
körív3 100 180
körív3 50 60
körív3 50 120
Ennek segítségével gyönyörű szivárványt is rajzolhatunk!
|
tanuld szivárvány |
 |
BEKÜLDENDŐ FELADATOK
1. FELADAT

|
Rajzolj hóembert! A teste három, egyre kisebb körből áll, a szeme és a gombjai kiszínezett, pici körök, a kezei vonalakból vannak rajzolva, a szája körív, az orra kitöltött háromszög. Vigyázz, hogy szépen és pontosan helyezd el az egyes részleteket! |
2. FELADAT

|
Rajzolj napot! Egy körlapból és sugarakból áll. A sugarakat úgy lehet megrajzolni, ha két körívet rajzolunk egymás után (lehet, hogy ehhez segédeljárásokra lesz szükségünk: jó, ha van egy jobbra rajzoló és egy balra rajzoló körív-eljárásunk, és ezeket használjuk egymás után). Majd a napsugár hegyénél majdnem teljesen visszafordulunk, és ugyanilyen két körívet rajzolunk egymás után. |
3. FELADAT
 óra 8 35  óra 5 12 |
Írj olyan eljárást, melynek két paramétere van, az óra és a perc, és olyan órát rajzol, mely pontosan mutatja a megadott időt! A kör és a beosztások megrajzolása mindig ugyanaz (a beosztásokhoz ki kell számolni a szöget, hogy középről indulva mennyit kell fordulni a következő beosztás megrajzolásához). Ami változik, az a mutatók helyzete. A percmutató helyzetének kiszámítása az egyszerűbb. A szöget kell kiszámítani, hogy a teknőcnek a függőlegeshez képest mennyit kell elfordulnia ahhoz, hogy a mutatót megrajzolja. Tudjuk, hogy a percmutató egy óra, azaz 60 perc alatt fordul 360°-ot, így nem nehéz kiszámolni, hogy az adott perc alatt mennyit fordul. A kismutató azonban nem ennyire egyszerű, mivel annak fordulása nem csak a megadott órák számától függ, hanem a perctől is, hiszen pl. 8 óra 35 perckor a kismutató nem pontosan a 8-ason áll, hanem a 8-as és 9-es szám között valahol. De vajon hol? A kismutató 60 perc alatt egy beosztásnyit megy előre, tehát arányosan ki kell számolni, hogy akkor az adott perc alatt mennyit fog előre menni, és ezt még hozzá kell adni ahhoz a szöghöz, amit az órák száma ad meg. |
| Vissza az oldal tetejére | Az érdekességekhez | ||
|---|---|---|---|
| Előző lecke | Következő lecke |