6. lecke - Spirálok

Ebben a leckében csigavonalakat,azaz spirálokat fogunk rajzolni. De hogyan?

Ahogy az ábrákon is látszik, ha csigavonalat szeretnénk rajzoltatni a teknőccel, nem kell neki mást mondani, minthogy menjen előre, majd forduljon jobbra, majd megint előre, majd megint forduljon jobbra, stb. Csak az a kérdés, hogy mennyit menjen és mennyit forduljon?

Próbáljuk ki, mi történik, ha a teknőc minden lépésben ugyanannyit megy előre és ugyanannyit is fordul! Ehhez használhatjuk az ismétlés parancsot. Ahhoz, hogy a csigavonal ne nézzen ki túl szögletesnek, inkább kereknek, nagyon pici lépéseket kell tennünk a fordulások között.

Lássuk tehát a következőt:

Ez bizony így egy kört rajzol. Próbáljuk ki más hosszal és fordulással:

Látható, hogy ha az ismétlés paranccsal próbálunk rajzolni, a teknőc mindenképpen kört rajzol.

Spirál rajzolásánál ugyanis az előre parancs után következő lépéshosszt minden lépésben egy kicsit növelni kellene. Ha a legegyszerűbb ábrát közelről megnézed, láthatod, hogy a fordulási szög ugyanaz minden lépésben, de a lépéshossz mindig nő egy keveset.

Próbáljuk ki a következőt:

Nos, Te is ilyen ábrát kaptál? (A spirál kevésbé látszik szögletesnek, ha a tollvastagságot kicsit megnöveled.)

Ez bizony már csigavonal! A következő kérdés csak az, hogyan tudnánk ezt eljárásban megírni, úgy, hogy ne kelljen ennyit írni. Vagyis egyszerűsíteni és rövidíteni kellene.

Ehhez egy olyan paraméterre van szükségünk, melynek értékét minden lépésben meg kell változtatni. Ezt az ismétlés paranccsal nem tudjuk megoldani, mivel annak segítségével csak pontosan ugyanazokat az utasításokat tudjuk ismételgetni, pontosan ugyanazokkal a paraméterekkel, változtatásra nincs mód.

Ezért van szükség a rekurzióra. A rekurzió azt jelenti, hogy egy (általában egyszerű) eljáráson belül meghívjuk ugyanazt az eljárást, vagyis saját magát megváltoztatott paraméterekkel. Az újonnan meghívott eljárás megint meghívja saját magát, majd megint és megint. Úgy, mint amikor beállsz két szembeállított tükör közé, és a tükörben így látod magadat és a tükröt kisebben, abban a tükörben megintcsak magadat és a tükröt még kisebben, és így tovább, egyre kisebben és kisebben a végtelenségig.

A rekurzív eljárás azonban nem tarthat a végtelenségig, valahogy bele kell írni, hogy meddig hívogassa meg saját magát. Ezért szükségünk lesz benne egy feltételre: az eljárás mindig csak akkor hívja meg önmagát, hogyha a feltétel teljesül, különben leáll.

A mi esetünkben a rekurzív eljárás abból áll majd, hogy a teknőc előre megy valamennyit, majd jobbra fordul. Ezután meghívja önmagát egy kicsit nagyobb lépéshosszal. Tehát egy kicsit többet megy előre, és jobbra fordul. Majd még többet megy előre, és jobbra fordul. Így rajzol spirált. Mindezt addig teszi, amíg a lépéshossz el nem ér egy megadott számot. A feltételünk tehát az lesz, hogy akkor hajtsa végre az utasításokat, ha a lépéshossz még nem nagyobb egy bizonyos számnál, pl. 30-nál. A lépéshosszt majd 1-gyel kezdjük, minden lépésben 1-gyel növeljük, addig, amíg 30-ig el nem ér. Így pontosan az előző ábrát kapjuk majd. Ezt a legegyszerűbb eljárást spirál0-nak neveztem el, a paramétert (a lépéshosszt) pedig lépés-nek.

Tehát az eljárás:

Nézzük meg egyesével, hogy mit is csinálnak az eljárás belsejében lévő utasítások:

ha :lépés <= 30 - ez a feltétel: csak addig hajtsa végre az utasításokat (amik a szögletes zárójelen belül vannak), amíg a lépéshossz el nem éri a 30-at.
előre :lépés - lépéshossznyit megy előre.
jobbra 20 - jobbra fordul 20°-ot.
spirál0 :lépés + 1 - meghívja saját magát a paramétert (lépéshosszt) 1-gyel növelve.

Mivel a spirál akkor lesz a legszebb, ha a lépéshosszt 1-ről kezdjük, ezt az eljárást mindig a spirál0 1 paranccsal kell meghívni. Ezért akár írhatunk egy főeljárást is, melynek nincs paramétere, és csak annyit tesz, hogy meghívja ezt az eljárást (a neve legyen főspirál0).

Ez a következőképpen néz ki:

Most már a főspirál0 paranccsal bármikor megrajzolhatod a spirált. Természetesen a tollszínt és tollvastagságot kedvedre változtathatod. Hosszabb csigavonalat is rajzolhatsz, ehhez a spirál0 eljárásban a feltételben szereplő számot kell megnövelni (pl. 30 helyett 40-re), így az eljárás többször hívja meg magát, és csak később áll le.

Sőt, mi lenne, ha a spirál nem egyszínű lenne, hanem színes?

Mit gondolsz, ezt a spirált hogy rajzoltam?

Látszik, hogy minden lépés után megváltoztattam a színt, mégpedig véletlenszerűen, a véletlenszám parancs segítségével. Ezt az új utasítást a spirál0 eljárás elejére kell beírni, tehát az eljárás így módosul:

Igaz, hogy eddig mindig a véletlenszám 16 parancsot használtuk a színválasztáshoz, de tudjuk, hogy az 0-tól 15-ig választ számot. A 15-ös szám azonban a fehéret jelenti, és most úgy szeretnék színt választani, hogy a fehér ne legyen köztük, mert az a fehér háttéren nem látszik. Ezért írtam véletlenszám 15-öt, mely csak 0-tól 14-ig választ egy számot, vagyis a fehéret sohasem választja.

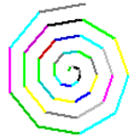
Játsszunk még egy kicsit a spirálunkkal! Mi történik, ha az elfordulás szögét változtatjuk meg az eljárásban?

Tudsz ilyeneket rajzolni?

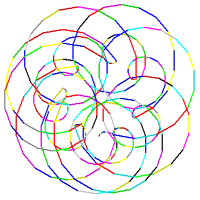
Megpróbálhatunk több ilyen spiráltis rajzolni ugyanabból a középpontból úgy, hogy közöttük elfordulunk valamennyit. Hátha gyönyörű spirálmintákat kapunk.

Próbáld ki a következőt: ismétlés 9 [főspirál0 jobbra 40] Nos, ez tényleg gyönyörű spirálminta, de ha jól megnézed, láthatod, hogy a spirálok nem egy pontból kezdődnek. Vajon miért?

A gond az, hogy a spirált mindig középről kezdjük rajzolni, de nem középen hagyjuk abba, hanem a végénél. Ahhoz, hogy ugyanabból a pontból kezdhessük a spirálokat, valahogy mindig vissza kell jutnunk középre. Ha a képernyő közepére rajzolunk, akkor ezt könnyen megtehetjük a haza parancs segítségével. E parancs hatására a teknőc mindig visszamegy a képernyő közepére, de vigyázz, ha nem emeled fel a parancs előtt a tollat, akkor vonalat is húz középig!

Lássuk tehát így: ismétlés 9 [főspirál0 tollatfel~ haza~ tollatle jobbra 40] Hogy tetszik?

Ki tudja a legszebb spirálmintát rajzolni? Változtasd meg az ismétlések számát, az elfordulás szögét, a kezdőpontokat!

Nemcsak apró szakaszokból lehet azonban spirált rajzolni, hanem bármilyen alakzatból. Ehhez segítségül hívjuk a 0. leckében megírt általános, szabályos sokszögeket rajzoló eljárásunkat. Ismételjük át, hogy is nézett ki:

Két paramétere van tehát: n, ami a sokszög szögeinek száma, és hossz, ami a sokszög oldalhosszát határozza meg. Háromszöget például a soksz 3 100, négyzetet a soksz 4 50, tízszöget a soksz 10 30 paranccsal rajzolhatunk.

A spirál megrajzolásakor pedig a kis szakaszokat most "láthatatlanul", azaz felemelt tollal rajzoljuk majd, minden kis szakasz végén pedig rajzolunk egy háromszöget, lépésenként növekvő oldalhosszal (az oldalhossz ugyanaz lesz, mint a lépéshossz).

Az új eljárást nevezzük spirál1-nek. Az első eljárásunkat kell csak kiegészíteni a toll felemelésével és a háromszögrajzolással: tanuld spirál1 :lépés tollszín! véletlenszám 15 ha :lépés < 40 [tollatfel ~ előre :lépés~ tollatle soksz 3 :lépés jobbra 20~ spirál1 :lépés + 1] vége

Ahhoz, hogy a legkisebb háromszögek is látsszanak a spirál közepén, nem muszáj 1-es lépésszámmal meghívni az eljárást, lehet 3-mal, 5-tel vagy akár 10-zel is. Próbáld ki, melyik a legszebb:

Amelyiket a legszebbnek tartod, arra akár írhatsz egy főeljárást is, pl:

Próbálj ki más sokszögeket is! Az oldalhosszuk lehet akár nagyobb is, maradhat állandó is, és a színt sem muszáj a véletlenszám paranccsal meghatározni, rajzolhatsz egyszínű csigavonalakat is.

Íme még két példa:

Ez a spirál négyzetekből áll, melyek oldalhossza a lépéshossz háromszorosa. tanuld spirál2 :lépés tollszín! 9 ha :lépés < 40 [tollatfel előre :lépés~ tollatle soksz 4 :lépés * 3 jobbra 20~ spirál2 :lépés + 1] vége

Ez pedig háromszögekből, melyek oldalhossza nem változik, mindig 100. tanuld spirál3 :lépés tollszín! 2 ha :lépés < 40 [tollatfel~ előre :lépés~ tollatle soksz 3 100 jobbra 20~ spirál3 :lépés + 1] vége

És Te tudsz hasonlókat?

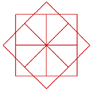
Mi történik, ha nem szabályos sokszögekethasználunk fel a spirálban, hanem kisebb mintákat, melyeket szabályos sokszögekből építünk fel? Például egy 8 négyzetből álló sokszögmintát (olyat, mint amiket az 1. leckében rajzoltunk), melyre először külön eljárást írunk:

tanuld minta :hossz ismétlés 8 [soksz 4 :hossz jobbra 45] vége

Ezután az eljárás: tanuld spirál4 :lépés tollszín! 4 ha :lépés < 40 [tollatfel előre :lépés~ tollatle minta :lépés jobbra 20~ spirál4 :lépés + 1] vége

Ezeket az eljárásokat is az előzőekhez hasonlóan, a kezdeti lépéshossz megadásával kell meghívni.

Ez a spirál már egész hasonló egy igazi tengeri csigaházhoz. Megpróbálhatunk közönséges csigához hasonló csigavonalat is rajzolni. Ennek egészen kereknek kellene lennie, vagyis a legjobb lenne, ha körökből állna. Nos, igazán szép kört csak nagyon nagy méretben tudnánk rajzolni, most kicsit csalni fogunk, és 36-szöget használunk helyette, mely nagyon hasonlít a körhöz. 36-szöget viszont egyszerűen a már meglévő soksz eljárásunkkal is tudunk rajzolni.

Így tehát az eljárás: tanuld spirál5 :lépés tollszín! 3 ha :lépés < 40 [tollatfel előre :lépés~ tollatle soksz 36 :lépés jobbra 20~ spirál5 :lépés + 1] vége

Vigyázz, ez a spirál hatalmas lesz, ha középről kezded, nem is biztos, hogy kifér a képernyőre!

1. FELADAT

Rajzold meg az ábrán látható spirált! Alkotóelemeire írj külön eljárást!

2. FELADAT

Rajzold meg az ábrán látható spirált! Alkotóelemeire írj külön eljárást!

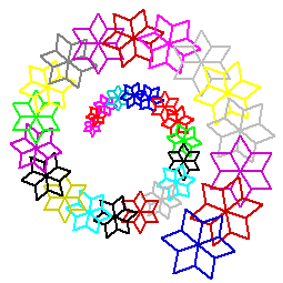
3. FELADAT

Rajzold meg az ábrán látható spirált! Alkotóelemeire írj külön eljárást!

4. FELADAT

Rajzolj saját spirálokat! Állhatnak sokszögekből vagy kisebb mintákból, lehetnek sokszínűek vagy egyszínűek, a lényeg, hogy minél változatosabbak legyenek!

	Vissza az oldal tetejére		Az érdekességekhez
	Előző lecke		Következő lecke