ÉRDEKESSÉGEK

A 7. LECKÉHEZ - FRAKTÁLOK

1. Fraktálok a természetben

Az itt felsorolt példák, ahogyan már korábban is említettük, nem igazi fraktálok, hiszen végesek, azonban mintázatuk láthatóan fraktálszerű, ezért kerültek ide.

Ilyen mintázat jellemzi a karfiolt, ... Forrás: http://www.ba.infn.it/~zito/project/nfractals.html

... a brokkolit, ... Forrás: http://commons.wikimedia.org/wiki/Image:Fractal_Broccoli.jpg

... fákat, ... Forrás: http://fractogene.com/full_genome/fractal_visual_gallery.html

... páfrányokat, ... Forrás: http://cordelia.mclean.org/~lowen/fractals.html

... az amerikai Grand Canyon-t. Forrás: http://cordelia.mclean.org/~lowen/fractals.html

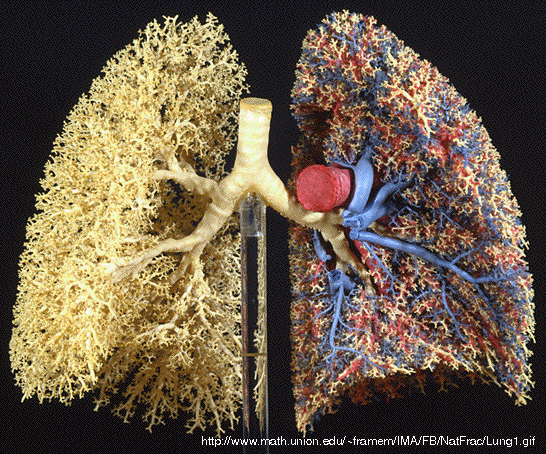
Az emberi tüdő... Forrás: http://fractogene.com/full_genome/fractal_visual_gallery.html

...és szív felépítése szintén fraktálszerű. Forrás: http://local.wasp.uwa.edu.au/~pbourke/fractals/images/heart.html

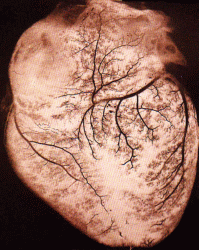
2. Fraktál-képek

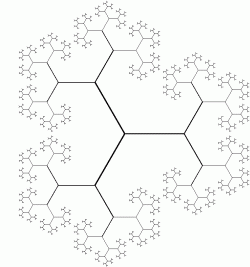
Ezen a fraktálon minden szög 120°-os, és a szakaszok rövidülnek, ahogyan távolodunk a középponttól. Bináris fraktálnak is nevezik, mert minden szakasz végpontjából két irányba haladhatunk tovább. Máshol méhkaptárként találkozhatunk vele, és ha jobban megnézzük felfedezhetőek a szabályos hatszögekre emlékeztető alakzatok. Forrás: http://mumble.net/~jar/visuals/fractal.html

A Mandelbrot-halmaz az egyik legismertebb fraktál. Forrás: http://www.integralscience.org/creation/creation.html

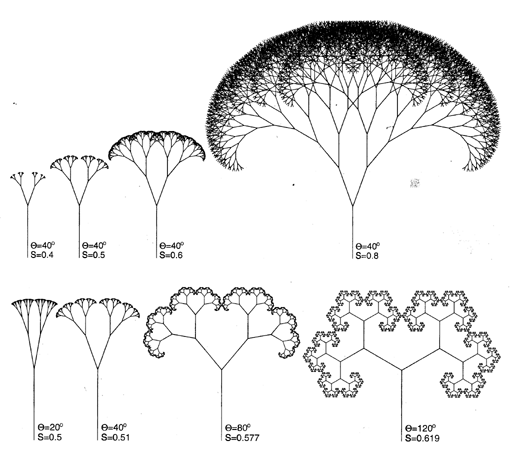
A mellékelt ábrán szereplő fraktál-fákon jól látható az egyes paraméterektől függő változás (ágak által bezárt szög, szakaszok aránya, mélységi szint). Forrás: http://www.td-grafik.de/artic/talk20030122/morphology_fractal.html

Az interneten rengeteg fraktál-galériát találunk, szebbnél-szebb színpompás számítógépes grafikákkal. Forrás: http://www.enchgallery.com/fractals/fractalpages/enchasketch.htm

3. Fraktálok különböző előállítási módszerei

I. A többlencsés fénymásológép

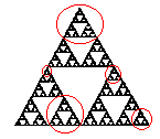
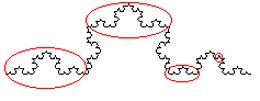
A fraktálok egyik legfontosabb tulajdonsága az önhasonlóság. Például a 7. leckében megismert fraktálok mindegyike szigorúan önhasonló, ami azt jelenti, hogy bármely részletüket nagyíthatjuk akár a végtelenségig, egyre újabb és újabb, az eredetihez szigorúan hasonló alakzatokhoz jutunk. Vizsgáljuk ezt meg néhány ábrán keresztül. Az alábbi ábrákon a bekarikázott részletek teljesen egyformák, csak méretükben térnek el egymástól.

Az elkövetkezőkben egy olyan előállítási módszerrel ismerkedhetünk meg, mely pontosan az önhasonlóságot használja ki.

Mindehhez egy képzeletbeli fénymásológépre lesz szükségünk, amely több lencsével dolgozik. Ez azt jelenti, hogy ha egy alakzatot lemásolunk, az több példányban másolódik le a papírra. Ezen kívül, ahogy a valódi fénymásolók esetében is, nagyítani és kicsinyíteni is tud előre beállított mértékben.

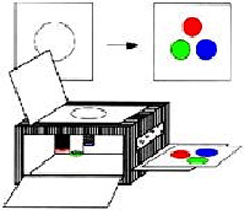
A fénymásolat kinézete attól függ, hogy hány lencsénk van (ennyi példányban másol), hogy azok hol helyezkednek el, és milyen arányban kicsinyítenek. Nézzük meg például egy háromlencsés fénymásológép működését egy körlemez másolása esetén, ha a kicsinyítés aránya 1/2, és a lencsék egy szabályos háromszög csúcsaiban helyezkednek el (a szemléltetés kedvéért a három lencse az első lépésben három különböző színnel fénymásol):

Nézzük meg, mi történik, ha egy ábrát (például egy négyzetet) ezzel a háromlencsés fénymásolóval lefénymásolunk, majd az eredményül kapott ábrát mindig újra és újra lefénymásoljuk (a fénymásoló csak az első lépésben másol három különböző színnel, azután már megtartja az eredeti színeket):

1. lépés	2. lépés	3. lépés
4. lépés	5. lépés	6. lépés

Látható, hogy eredményül a Sierpinski-háromszöget kapjuk. (Természetesen az "igazi" Sierpinski-háromszöget csak végtelen lépés után kapnánk meg.)

Ezt a módszert akár kézzel rajzolva is könnyen kipróbálhatjuk. Egyszerűbb dolgunk lesz, ha nem az előbbi ábrán látható négyzetből, hanem egy szabályos háromszögből indulunk ki. Ennek csúcsait használva a kicsinyítés középpontjának kicsinyítsük le önmagát, és a kapott kisebb háromszöget színezzük be. Az ábrán bemutatjuk mindhárom csúcshoz való kicsinyítés eredményét külön-külön, majd pedig az eredményt.

A következő lépésben a most kapott ábrát kicsinyítsük a szabályos háromszög csúcsaihoz. Ha ezt az eljárást tovább folytatjuk az egyes lépésekben kapott ábrákkal, már néhány lépés után látszik, hogy az eljárás a Sierpinski-háromszöget adja eredményül.

1. lépés

2. lépés

Ugyanezzel a módszerrel előállíthatjuk például a Cantor halmazt is. Induljunk ki egy szakaszból, majd kicsinyítsük 1/3 arányú kicsinyítéssel ezt a szakaszt saját végpontjaihoz.

Milyen ábrából induljunk ki?

Az előbbiek szerint tehát könnyedén előállíthatjuk a korábban megismert fraktálok legtöbbjét, ha tudjuk, mi legyen a kiindulási ábra, és milyenek legyenek a kicsinyítések (középpontjuk és arányszámuk), illetve hány darab kicsinyítés kell. De vajon tényleg szükségünk van minden adatra? Az előző ábrák összehasonlításával sejthető, hogy a válasz "nem", hiszen először egy négyzet, utána pedig egy szabályos háromszög volt a kiindulási ábra, mégis mindkét esetben a Sierpinski-háromszöget kaptuk eredménynek. Lehet, hogy teljesen mindegy, milyen ábrából indulunk ki? Lássunk néhány példát!

Próbáljuk meg előállítani a Cantor-halmazt a "Cantor" feliratból!

Vagy a Sierpinski-háromszöget önmagából, egy nagy pöttyből, egy kriksz-krakszból vagy egy rózsából!

Ugye, milyen meglepő? Úgy tűnik, bármilyen ábrából kiindulhatunk, a speciális fénymásológép már néhány lépés után olyan kicsire kicsinyíti a kiindulási ábrát, hogy az nem felismerhető többé. Csak az függ a kiindulási ábrától, hogy az eredményül kapott fraktál hány lépés után kezd felismerhetővé válni. Ezek után sejthető, hogy a többlencsés fénymásológép bármilyen kiindulási ábrából ugyanazt a fraktált állítja elő, ha jól állítjuk be a lencséket.

II. A Sierpinski-háromszög és a Pascal-háromszög

A következő fraktál-előállítási módszerhez a Pascal-háromszögre lesz szükségünk. A Pascal-háromszög számokból áll, és a csúcsától kezdve tudjuk könnyen felírni. Kezdjük egy 1-essel, tőle balra és jobbra lefelé írjunk még egy-egy 1-est. Ezután az újabb sor számai úgy jönnek ki, hogy összeadjuk a felettük található két számot. (A sor elején és végén lévő számok fölött csak egy szám van, így csak az számít.) Az alábbi ábra mutatja a Pascal-háromszög első 17 sorát, de természetesen a végtelenségig lehetne folytatni.

Nos, hogy lesz ebből fraktál? Az általunk ismert klasszikus fraktálok közül a Sierpinski-háromszöget tudjuk a Pascal-háromszögből elővarázsolni. A "varázslat" pedig igen egyszerű: színezzük feketére a Pascal-háromszögben a páratlan számokat. Íme az eredmény:

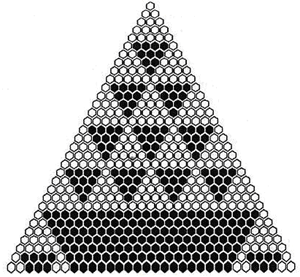
Próbáljuk ki, hogy vajon akkor is ilyen szabályos, önhasonló mintázatot kapunk-e, ha más szám szerinti oszthatóság alapján színezzük ki a Pascal-háromszög elemeit. Tegyünk néhány próbát, és színezzük feketére a 3-mal, 5-tel, 9-cel oszthatószámokat! Ahogy a következő ábrákon látható, ezekben az esetekben is tökéletesen önhasonló fraktált kapunk.

3-mal osztható számok színezése	5-tel osztható számok színezése

9-cel osztható számok színezése

III. A káosz-játék

A káosz-játékhoz szükségünk lesz egy papírra, egy ceruzára, egy vonalzóra és egy dobókockára. A játékszabályok a következők: kiindulásképpen rajzoljunk három, egy szabályos háromszög csúcsaiban elhelyezkedő pontot, ezek lesznek az alappontok, számozzuk meg őket 1-től 3-ig. Rajzoljunk egy negyedik pontot akárhová a papíron, ez lesz a kiindulópont. Kockadobás segítségével válasszunk ki egy alappontot a következő szabályok szerint: ha 1-est vagy 2-est dobunk, akkor válasszuk az 1-es alappontot, ha 3-ast vagy 4-est dobunk, akkor a 2-es alappontot, és ha 5-öst vagy 6-ost, akkor a 3-ast. Illesszük a vonalzót a kiválasztott alappontra és a kiindulópontra, és távolságuk felénél rajzoljunk újabb pontot. Majd folytassuk a játékot az új ponttal ugyanígy. Az alábbi ábrán látható az első néhány lépés:

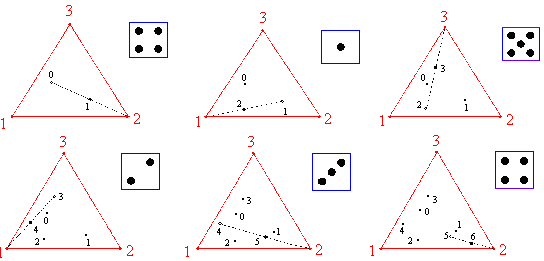
(Az ábrán az alappontok össze vannak kötve egymással, hogy ne tévesszük őket össze a kapott pontokkal).

Elég sokáig játszva a játékot, ismerős ábra rajzolódik ki a szemünk előtt:

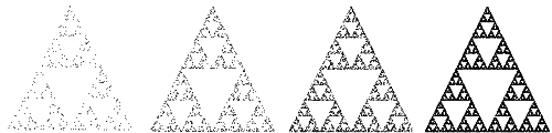
Első ránézésre meglepőnek tűnhet, de jól látszik, hogy (végtelen lépés után) a Sierpinski-háromszöget kapjuk végeredményül. Ez azonban korántsem meglepő, ha közelebbről megvizsgáljuk, mi is történik pontosan a játék folyamán.

Először is új pontot mindig úgy kapunk, hogy a régi pont távolságát egy csúcstól felére csökkentjük; a leglényegesebb észrevétel az, hogy ez másképpen fogalmazva egy 1/2 arányú kicsinyítés elvégzése a ponton a csúcsból. Ez azt jelenti, hogy ugyanazt tesszük, mint a többlencsés fénymásológép, mely a Sierpinski-háromszöget előállította, azzal a különbséggel, hogy mindig csak egyetlen pontot kicsinyítünk egy egész ábra helyett, és nem mindhárom csúcshoz, csak az egyikhez. Emiatt a folyamat sokkal lassabb, és csak többszáz vagy többezer lépés után látszik igazán jól a Sierpinski-háromszög, míg a fénymásoló esetén már 4-5 lépés is elegendő volt.

Vajon a többi, általunk megismert fraktált is elő lehet-e állítani káosz-játékkal, ha megfelelően változtatnánk a játékszabályokon? A válasz természetesen igen, a klasszikus fraktálokra könnyen meghatározható a játékszabály is. Például a Cantor-halmazhoz két alappontra van szükségünk, és 1/3-os kicsinyítésre (azaz a kiválasztott alappont és az éppen játékban lévő pont távolságát mindig harmadolni kell, így kapjuk meg az új pontot), a Sierpinski-szőnyeghez négy alappontra egy négyzet csúcsaiban, és szintén 1/3-os kicsinyítésre, a Koch-görbéhez egy szimmetrikus, 3 egyenlő oldalú trapéz csúcsaiban elhelyezkedő négy alappontra és 1/3-os kicsinyítésre. Ha ismerjük az egyes fraktálokat előállító többlencsés fénymásológép működését, akkor könnyen meghatározhatjuk a káosz-játék szabályát: annyi alappont kell, ahány lencséje van a fénymásolónak, és az alappontoknak ugyanúgy is kell elhelyezkedniük, mint ezeknek a lencséknek. A szabály pedig pont ugyanaz a kicsinyítés, amit a fénymásoló végez.

A klasszikusfraktálokról az alábbi oldalakon olvashatsz:

Cantor-halmaz:

Angol nyelvű oldalak képekkel, animációkkal:

Koch-görbe, Koch-hópehely:

Angol nyelvű oldalak képekkel, animációkkal:

Sierpinski-háromszög:

Angol nyelvű oldalak képekkel, animációkkal:

Sierpinski-szőnyeg, Menger-szivacs:

Angol nyelvű oldalak képekkel, animációkkal:

Peano-görbe:

Angol nyelvű oldalak képekkel, animációkkal:

A Pascal-háromszög színezése oszthatóság szerint:

A káosz-játék:

Angol nyelvű oldalak képekkel, animációkkal:

	Vissza az oldal tetejére		Vissza a leckéhez